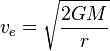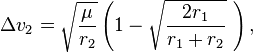One of the most important parts of the development of any interplanetary mission is trajectory planning. The exact trajectory the spacecraft takes affects several factors, including travel time, delta-V needed, thermal and radiation environment, and more. Given that Mercury is quite far from Earth, and in a very different orbit, trajectory analysis will be especially important for this mission.
Previous unmanned missions to Mercury, such as Mariner 10 and MESSENGER, used multiple flybys of Venus and Earth to reduce the amount of delta-V needed. However, I won't be using them for this mission. First, using flybys, while reducing delta-V, usually increases the travel time greatly; the MESSENGER probe took about four years to arrive at Mercury. Since this is a manned mission, we want to ensure that our astronauts do not spend any longer in space than they have to. Second, NASA has some of the best supercomputers in the world available to do the highly complex calculations needed for planning flyby trajectories. I have an old laptop and a graphing calculator. So, instead, our trajectory will be as direct as possible of a transfer from Low Earth Orbit to Mercury's surface (and back).
Some of the orbital parameters of Mercury and Earth can be found here: http://nssdc.gsfc.nasa.gov/planetary/factsheet/mercuryfact.html.
It becomes immediately apparent that there are several problems. Mercury's orbit is inclined about 7 degrees, compared to virtually nil for Earth. This means that a planar change will be required, significantly increasing the delta-V requirements. Mercury's orbit is also highly eccentric, with the perihelion and aphelion more than 20 million kilometers apart. In order to minimize the delta-V required, we should try to intercept Mercury near its aphelion.
According to this site, roughly 17 km/s of delta-V is required for an Earth to Mercury transfer. However, the results given there are approximate, and don't account for plane changes or any other factors. I'd prefer to do the numbers myself. First, we'll calculate the delta-V needed to transfer from Earth's orbit to Mercury (neglecting the velocity needed to escape from Earth's gravitational pull). This is known as the "excess hyperbolic velocity", it's called that because the escape trajectory looks like a hyperbola relative to Earth (orbits with an eccentricity greater than 1 are hyperbolas, while those with e<1 are ellipses). We'll assume that a single burn is done that changes our orbit from one that is the same as Earth's to one that intersects Mercury's at aphelion (which will be our new perihelion).
From that fact sheet I linked earlier, Earth has a mean orbital velocity of 29.78 km/s (our planet's orbit is nearly circular, the min and max are only about a kilometer apart). The orbital radius of Earth's orbit is 1.496*10^8 kilometers, while Mercury's orbital distance at aphelion is 6.98*10^7 kilometers. Since both bodies (and our hypothetical spacecraft) are in solar orbit, the value of μ (the standard gravitational parameter) is 1.327*10^20 m^3/s^2. Substituting these into the equation for the delta-v of the first burn for a Hohmann transfer orbit
we see that a delta-v of 6026 m/s is needed. Note that since we're moving inward from Earth, we actually have to slow down our craft by that much. This value of 6026 m/s is our excess hyperbolic velocity. We'll call it 6.1 km/s, since there might be a few uncertainties and simplifications I've done that could add a couple m/s.
Next, we have to account for the velocity needed to escape Earth. That's given by the following formula;
Computing this for an escape from Earth's surface will give a value of about 11 km/s. However, our mission will start in Low Earth Orbit, a few hundred kilometers above Earth's surface. Since it's in orbit, it will already be traveling at very high speed. This means that our delta-V needed will be less than what is given by the formula. Assuming a 300 km parking orbit; our escape velocity will be approximately 10.93 km/s. However, at a 300 km orbit, our orbital velocity is about 7.73 km/s, so we only need ~3.2 km/s to escape from Earth's gravitational pull. If we simply added this to our excess hyperbolic velocity, we would get that we need a delta V of almost 10 km/s at Earth departure. Fortunately, this is not the case;
Computing the value for "v" given our known escape velocity and excess hyperbolic velocity, we get a delta V of roughly 6.9 km/s.
Our calculations for Earth departure are complete except for one step; accounting for the difference in inclination between Earth's orbit an Mercury's orbit. Mercury's orbit is inclined 7 degrees relative to Earth's; failing to account for this would result in our spacecraft missing its destination by millions of kilometers.
If we perform the inclination change immediately after our burn to leave Earth, our needed delta V would be given by the following formula;
Changing our inclination to completely match Mercury's would require an additional delta V of about 2.9 km/s. On the other hand, if we were able to time our launch such that we only had to change our inclination by 3 degrees to intercept Mercury, only 1.25 km/s of delta V would be required. In the second case, our total Earth departure delta V would come to about 8.2 km/s.
The procedure to compute the delta V upon arrival at Mercury is essentially the same as the one for Earth departure, only in reverse.
We will plan on entering a 100 km parking orbit around Mercury. In order to become captured by Mercury's gravity, we must eliminate all velocity relative to the planet, less our orbit speed in the parking orbit (we will assume the capture burn takes place at our point of closest approach to Mercury). In a 100 km parking orbit around Mercury, our orbital speed will be 2.94 km/s. Looking at the Hohmann transfer orbit equations, we see that the velocity needed to match Mercury at aphelion from our transfer orbit is given by the following;
Running the numbers, we get that a delta V of 7.31 km/s is needed. It would appear then, that our capture velocity is given by (7.31-2.94) = 4.37 km/s. However, while becoming captured, we will be going deeper into Mercury's gravity well, trading gravitational potential energy for kinetic energy. This will require additional delta V to cancel, equal to the escape velocity from an altitude of 100 km above Mercury; 4.16 km/s. Therefore, our total deltaV at capture is 8.51 km/s. Combining this with our Earth departure deltaV, we see that our total delta V needed to travel from Low Earth Orbit to Low Mercury Orbit is approximately 16.7 km/s, which we can round up to 17 km/s.
Scram Cannon
Monday, December 14, 2015
Monday, November 23, 2015
Manned Mercury Mission - Part 01 - Introduction
There's been quite a lot written about manned Mars missions. Missions to Mars show up in Hollywood movies, news articles, and are even planned for the 1980s 1990s 2000 2020s 2030s. It looks like the logical next step after the moon; it's pretty close, has a nice red color, liquid water (sometimes), and might even have had life once! It's no wonder that so many people are fascinated by it. Still, I don't plan on doing a rehash of a bunch of stuff that's already been written by quite knowledgeable people, so I'm not going to be writing about manned Mars missions here.
Less well known are the plans for manned Venus missions. Venus is the closest planet to Earth, but that's about all it has going for it. Temperatures on the surface are hot enough to melt lead, and the pressure would crush a man instantly. The atmosphere is composed mostly of carbon dioxide and sulfuric acid; definitely not a life-friendly environment. Despite this, there were planned for manned flybys as far back as the 1970s. The American plan would have used Apollo hardware, while the Soviets would have used an uprated N1 (the N1F) with a heavily modified Soyuz as the crew module. Neither plan came to fruition (due to budgets cuts / changing priorities in the American case, and the failure of the N1 for the Soviets). Instead; we (mostly the Soviets) sent dozens of unmanned probes; mapping the surface from orbit, investigating the atmosphere, and parachuting in landers that lasted for minutes at a time. Despite the inhospitability of the planet, you'll occasionally hear about plans for missions to Venus; some of them even include deploying blimps in the upper atmosphere (there are a some layers of the Venusian upper atmosphere where the temperatures are survivable).
Far less has been written about manned missions to Mercury. That planet is farther away from Earth than Venus or Mars. Also, it's a lifeless, barren rock; with no atmosphere to speak of, the sunward side is roasted, while the night side experiences cryogenic temperatures for weeks at a time. Mercury's magnetic field is horribly weak compared to Earth's, meaning that the surface is exposed to obscene amounts of radiation (this is also why Mercury can't retain an atmosphere). Far less is known about Mercury than other nearby planets; the first probe (Mariner 10) did flybys in the 1970s. The MESSENGER orbiter expanded mankind's knowledge of Mercury greatly, but compared to the Moon, Mars, or Venus, there's still many unanswered questions.
While a manned mission to Mercury would be highly difficult, it would certainly be possible with future technology. In fact, it could probably be done by 2050, assuming sufficient funding and will were available. While that's unlikely to happen (indeed, there are far better targets for exploration), it's still an interesting problem to look at.
Less well known are the plans for manned Venus missions. Venus is the closest planet to Earth, but that's about all it has going for it. Temperatures on the surface are hot enough to melt lead, and the pressure would crush a man instantly. The atmosphere is composed mostly of carbon dioxide and sulfuric acid; definitely not a life-friendly environment. Despite this, there were planned for manned flybys as far back as the 1970s. The American plan would have used Apollo hardware, while the Soviets would have used an uprated N1 (the N1F) with a heavily modified Soyuz as the crew module. Neither plan came to fruition (due to budgets cuts / changing priorities in the American case, and the failure of the N1 for the Soviets). Instead; we (mostly the Soviets) sent dozens of unmanned probes; mapping the surface from orbit, investigating the atmosphere, and parachuting in landers that lasted for minutes at a time. Despite the inhospitability of the planet, you'll occasionally hear about plans for missions to Venus; some of them even include deploying blimps in the upper atmosphere (there are a some layers of the Venusian upper atmosphere where the temperatures are survivable).
Far less has been written about manned missions to Mercury. That planet is farther away from Earth than Venus or Mars. Also, it's a lifeless, barren rock; with no atmosphere to speak of, the sunward side is roasted, while the night side experiences cryogenic temperatures for weeks at a time. Mercury's magnetic field is horribly weak compared to Earth's, meaning that the surface is exposed to obscene amounts of radiation (this is also why Mercury can't retain an atmosphere). Far less is known about Mercury than other nearby planets; the first probe (Mariner 10) did flybys in the 1970s. The MESSENGER orbiter expanded mankind's knowledge of Mercury greatly, but compared to the Moon, Mars, or Venus, there's still many unanswered questions.
While a manned mission to Mercury would be highly difficult, it would certainly be possible with future technology. In fact, it could probably be done by 2050, assuming sufficient funding and will were available. While that's unlikely to happen (indeed, there are far better targets for exploration), it's still an interesting problem to look at.
Monday, November 9, 2015
RD-0410
 |
| http://www.cosmoworld.ru/spaceencyclopedia/programs/yard.jpg |
 |
| via Astronautix |
The history of American efforts to develop nuclear thermal rockets is relatively well known. Similar Soviet efforts have remained far more obscure. However, during the Cold War, the Soviet Union developed and tested an advanced nuclear thermal rocket engine, designated the RD-0410. Unfortunately, relatively little English-language information about the RD-0410 can be found (at least in easily available sources).
Similar to the American NERVA program, development of Soviet
nuclear rocketry began in the mid-1950s. Serious research began in 1955, with
development of a rocket beginning in 1956 (the people working on this project
included such notable people as Kurchatov, Keldysh, and Korolev). Initially,
the Soviets planned to use the nuclear rocket to power an intercontinental
ballistic missile, or possible a cruise missile. However, it was quickly
realized that chemical rockets were good enough for suborbital flights. As a
result, by the 1960s, it was decided to develop the engine for usage in space.
The engine was developed by the KBKHA bureau, which had also
developed engines such as the RD-0105 (used on some derivatives of the R-7). The
goal was to develop an engine with a specific impulse of roughly 800-900
seconds, double what can be achieved with normal chemical rockets. Doing this
would require creating a nuclear reactor that was both very light, and capable
of withstanding very high temperatures around 3000 Kelvin. I have seen a few
references to a program to develop a 2,000 isp engine, but this would require
temperatures (over 15,000K) well in excess of what was possible in the 1950s
(or even today) for a solid core design.
The test site selected for the Soviet nuclear engine was
Semipalatinsk in Kazakhstan, a remote location similar to Jackass Flats in Nevada.
The Soviets had already tested numerous atomic weapons (including their first
in 1949 there), so the place was no stranger to nuclear activity. It appears
that tests of the engine were conducted in a mine shaft approximately 150
meters deep, unlike the American NERVA, which was tested aboveground. Most
likely, this was due to concerns over radiation should the engine malfunction.
At some point, the engine acquired the designation RD-0410, it is less commonly
known by its GRAU designation 11B91. That the engine received a GRAU
designation means that it was almost certainly considered for military
applications.
The American NERVA had a thrust of approximately 330
kilonewtons. This was much more than the RD-0410, which had about 35
kilonewtons. This was both by design, and due to political/monetary
considerations. The Soviet government had somewhat lost interest in the project
once it had become apparent that the nuclear engine was not usable as an ICBM
upper stage. More importantly, by developing a lower power engine, the reactor
assembly as a whole would be smaller. The RD-0410, including propellant, was
planned to mass roughly 15 tons when completed; putting it well within the
payload capabilities of Soviet launchers like Proton. The actual engine itself
weighed only about two tons. In contrast, the American NERVA was much heavier,
and could only be launched by a Saturn V or similar vehicle.
There were other important differences between NERVA and
RD-0410. The NERVA’s fuel elements were hexagonal in cross section, with
several holes drilled in them for hydrogen to pass through. Hundreds of these
elements (each about an inch wide) made up the NERVA’s reactor.
.png/623px-NERVA_fuel_element_configuration_(fr).png) |
| NERVA Fuel Elements |
It has been
difficult to find exact information about the geometry of the RD-0410’s fuel
rods, however, it appears that they had a complex shape. The fuel rods were
twisted, and had a complex cross section, shaped like the petals of a flower.
This was intended to lock the fuel rods together, and prevent fuel from falling
out of the reactor if a few rods cracked or became dislodged. The fuel elements
were made of uranium carbide, in order to better withstand the high
temperatures of the core.
Development and testing of the RD-0410 proceeded slowly. By
1973, America’s NERVA had already been test fired, then cancelled before
actually flying. However, large scale tests of the RD-0410’s components did not
begin until 1978. The test reactor was first started on March 27, 1978, and ran
for 70 seconds. Gradually, the reactor was run for longer, and at higher
temperatures. By 1981, the RD-0410 was running for an hour, its design
duration. A specific impulse of 910 seconds was achieved; this was superior to
that which was obtained with NERVA. The American Timberwind/SNTP project from
the late 1980s planned to achieve similar efficiency with much higher thrust to
weight, but it encountered numerous technical problems and did not reach the
test stage.
All accounts of the RD-0410 state that it’s testing at Semipalatinsk
went very well. Originally, it was planned that the engine would fly in 1985 (likely
replacing the Block D 4th stage on Proton). However, as the Soviet
Union imploded during the 1980s, development slowed, then halted. Other Soviet
nuclear rockets were planned, such as the RD-0411; a high thrust (~400 kN)
engine that would have been used on a Mars mission, and an engine designated
11B97, which would have had the capability of either nuclear thermal or
electric propulsion. However, like all other nuclear rocket programs, none of
them came to be.
 |
| via Astronautix, a concept for a Soviet Mars spacecraft, that likely would have used RD-0411 |
Bibliography:
http://www.cosmoworld.ru/spaceencyclopedia/programs/index.shtml?yard.html
Thursday, October 15, 2015
A Brief Primer on NTR Designs
As y'all probably know, I'm quite fond of the Nuclear Thermal Rocket. It has high performance and can be made using current technology (they actually tested some back in the 60s). I legitimately believe it's one of the best options for manned exploration beyond low Earth orbit.
Of course, NTRs are a pretty broad category. That term encompasses everything from solid core designs like NERVA to the nuclear light bulb. So, here's a brief primer on some of the basic designs, and some of their important features.
First, the open-cycle, solid core design.
It's fairly simple: pass hydrogen (or whatever fuel, but hydrogen is usually best) over the fuel rods of an operating nuclear reactor. The hydrogen heats up and is expelled out the rocket nozzle at high velocity. This is what the NERVA designs and their Soviet counterparts used. Thrust to weight is decent; much worse than a chemical rocket, but far superior to an ion engine. Specific impulse is around 800-900 seconds, maybe up to 1100 if you use better materials. The main limitation is the reactor temperature; above a certain temperature, your fuel rods will melt. Most concepts I've seen have the reactor operating at a maximum temp of about 3,000 K.
Next, the closed cycle, solid core design. I haven't seen much written about this one at all. Essentially, you separate your propellant and the radioactive bits (such as by putting a transparent window between them). Assuming the reactor operates at 3,000 K, most of you emissions are going to be in the infrared.
So, the radiation is going to pass through an IR transparent window, and then heat up the propellant. The advantage of this is that you don't risk having radiation in the exhaust. However, that's already a low concern for solid core designs, and closed-cycle solid is going to be heavier and have less efficient energy transport. I doubt you'll see one of these built anytime soon.
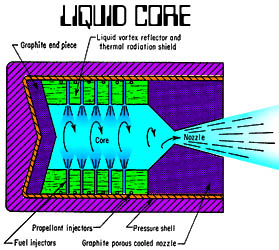
Next is the liquid-core NTR. Something of an intermediate step between solid and gas core designs; you heat up the uranium hot enough that it liquefies; this lets you get hotter temperatures and more energy out of your propellant. Of course, you have to contain the fuel; either by using a closed cycle design, or some other method. Possibly spinning the reactor at high speed like a centrifuge (the uranium will go to the outside, while the lighter hydrogen stays in the middle). Again, I haven't seen as much written about this one, though Atomic Rockets has a bit on it.
Performance would probably be somewhere inbetween solid and gas core designs, ballpark about 1,500-2,000 seconds of isp.
Next come the gas core designs. First, the open cycle. Heat up your fuel so hot it gasifies (well over 5,000K, possibly even over 20,000 K). Keep your fuel confined somehow (by centrifuging again, or injecting the propellant and fuel carefully), you'll still lose a bit anyway. Let the propellant pass directly over the fuel, so your heat transfer is very efficient. Above 4500K (the gas core is much hotter), diatomic H2 will dissociate, giving you another 40% or so bonus on your specific impulse.
Specific impulse for this one could be well north of 3,000 seconds (I've seen figures near 10k isp quote). Decent thrust, too. Shame about the radioactive exhaust.
Which is where the closed cycle gas core comes in. Also known as the nuclear lightbulb.
As you can see, it's pretty complex. Not only do you have to have some sort of material transparent to UV radiation (which is what your gasified fuel is going to be emitting), but you also have to keep it from melting. Absent finding a material that can withstand 50,000K temperatures, you have to cool it somehow. Luckily, LH2 is cryogenic, so you can just use your propellant as coolant. The performance is going to be a bit lower than an open-cycle design (since your weight is higher, and you'll have a bit less efficient heat transfer), but it more than makes up for this by not spewing fission products out the exhaust. In my opinion, this and NERVA are the ways to the future.
Of course, NTRs are a pretty broad category. That term encompasses everything from solid core designs like NERVA to the nuclear light bulb. So, here's a brief primer on some of the basic designs, and some of their important features.
First, the open-cycle, solid core design.
It's fairly simple: pass hydrogen (or whatever fuel, but hydrogen is usually best) over the fuel rods of an operating nuclear reactor. The hydrogen heats up and is expelled out the rocket nozzle at high velocity. This is what the NERVA designs and their Soviet counterparts used. Thrust to weight is decent; much worse than a chemical rocket, but far superior to an ion engine. Specific impulse is around 800-900 seconds, maybe up to 1100 if you use better materials. The main limitation is the reactor temperature; above a certain temperature, your fuel rods will melt. Most concepts I've seen have the reactor operating at a maximum temp of about 3,000 K.
Next, the closed cycle, solid core design. I haven't seen much written about this one at all. Essentially, you separate your propellant and the radioactive bits (such as by putting a transparent window between them). Assuming the reactor operates at 3,000 K, most of you emissions are going to be in the infrared.
So, the radiation is going to pass through an IR transparent window, and then heat up the propellant. The advantage of this is that you don't risk having radiation in the exhaust. However, that's already a low concern for solid core designs, and closed-cycle solid is going to be heavier and have less efficient energy transport. I doubt you'll see one of these built anytime soon.
Next is the liquid-core NTR. Something of an intermediate step between solid and gas core designs; you heat up the uranium hot enough that it liquefies; this lets you get hotter temperatures and more energy out of your propellant. Of course, you have to contain the fuel; either by using a closed cycle design, or some other method. Possibly spinning the reactor at high speed like a centrifuge (the uranium will go to the outside, while the lighter hydrogen stays in the middle). Again, I haven't seen as much written about this one, though Atomic Rockets has a bit on it.
 |
| (picture via Atomic Rockets page) |
Performance would probably be somewhere inbetween solid and gas core designs, ballpark about 1,500-2,000 seconds of isp.
Next come the gas core designs. First, the open cycle. Heat up your fuel so hot it gasifies (well over 5,000K, possibly even over 20,000 K). Keep your fuel confined somehow (by centrifuging again, or injecting the propellant and fuel carefully), you'll still lose a bit anyway. Let the propellant pass directly over the fuel, so your heat transfer is very efficient. Above 4500K (the gas core is much hotter), diatomic H2 will dissociate, giving you another 40% or so bonus on your specific impulse.
Specific impulse for this one could be well north of 3,000 seconds (I've seen figures near 10k isp quote). Decent thrust, too. Shame about the radioactive exhaust.
Which is where the closed cycle gas core comes in. Also known as the nuclear lightbulb.
As you can see, it's pretty complex. Not only do you have to have some sort of material transparent to UV radiation (which is what your gasified fuel is going to be emitting), but you also have to keep it from melting. Absent finding a material that can withstand 50,000K temperatures, you have to cool it somehow. Luckily, LH2 is cryogenic, so you can just use your propellant as coolant. The performance is going to be a bit lower than an open-cycle design (since your weight is higher, and you'll have a bit less efficient heat transfer), but it more than makes up for this by not spewing fission products out the exhaust. In my opinion, this and NERVA are the ways to the future.
Sunday, September 27, 2015
Atmospheric Flight on Titan
One of the first questions that must be solved when designing an aircraft for Titan is the propulsion system. Obviously, a simple chemical rocket could be used. One attractive propellant combination would be a methane/LOX engine. Water ice is believed to exist in quantity below the surface of Titan, and from this LOX can be made. Though the majority of the atmosphere of Titan is nitrogen, methane is also present, and the quantity increases at lower altitudes (up to about 4-5%). The surface hydrocarbon deposits also contain massive amounts of methane, as well as other hydrocarbons such as ethane and propane, which could be used as fuel or refined into methane.
However, chemical rockets are inefficient, so what other options are there? One exotic option, suitable for a large aircraft, would be a nuclear turbine, similar to the J87. Operation would be very similar to on Earth: the incoming Titanian atmosphere would be heated by the nuclear reactor, then expelled at high speed, producing thrust. This concept would have the advantage of virtually infinite range (though this would be of somewhat less consequence on a small body such as Titan). However, the mass of the reactor and shielding would severely cut into payload, making this method only suitable for a very large aircraft.
Aircraft on Earth carry their fuel with them, and harvest oxidizer from the atmosphere. What if we reversed this? What if our hypothetical Titanian aircraft instead harvested fuel from the environment, while carrying its own oxidizer?
We will use liquid oxygen (LOX) as our oxidizer, and methane as our fuel. The atmosphere of Titan has a pressure of about 146 kPa at the surface, and about 4% of this is methane. This means that the partial pressure of methane at the surface is roughly 5-6 kPa. This is close to the partial pressure of oxygen in Earth's atmosphere at an altitude of 10,000m. Given that operation of conventional jet engines is possible and that altitude is possible on Earth, it is reasonable to assume that there will be enough methane for our engine to operate on Titan, at least at low altitudes.
Analysis of the properties of methane indicates that it will be liquid at Titan's surface. On the other hand, nitrogen exists as a gas in Titan's atmosphere. This is useful; through careful design of the inlet, it would be possible to separate the methane fuel from the useless nitrogen. With the methane obtained, and liquid oxygen carried on board, our engine would function similar to a liquid air cycle engine. (More info on this type of engine can be found here). Though the specific impulse of the engine itself would be approximately the same as a conventional methane/liquid oxygen engine, the elimination of the need to carry fuel would dramatically increase payload and efficiency.
Alternatively, rather than separating methane out from the nitrogen, the Titanian atmosphere could be inducted in a gaseous state. This would allow a Brayton cycle engine to be used, as is done in a conventional jet turbine (LOX would again be used as the oxidizer). Though I have not yet done the math, it seems to me as though this would offer increased efficiency over the previous option (the Liquid Methane Cycle Engine?), though less thrust. Which option is better for our far-future Titanian aircraft would depend on the specific application.
Wednesday, September 9, 2015
Air Superiority F-106 - Pulling Out All the Stops
Months ago, I wrote a piece on the feasibility of the F-106 Delta Dart as an air superiority fighter. I ultimately came to the conclusion that the F-106 could, with slight modifications, serve as a decent multirole aircraft. But what if we made more than slight modifications?
Suppose that, at sometime around 1980 a country using the F-106 wanted to modify them such that they could be used in the air superiority role for at least another decade. How would they go about doing this?
Those of you who are more reasonable might ask why the country in question doesn't just buy a bunch of upgraded F-4s or MiG-23s (or even some F-15s or 16s) and use them instead. Well, they could, but that would be a quite boring end to this post.
I'm going to use the development of the Atlas Cheetah as a model for our F-106 improvement program. The Cheetah was developed by apartheid-era South Africa from their existing Mirage III airframes, and involved a quite extensive rework of the aircraft, including a complete rebuild of the airframe, fitting of an upgraded engine (in the Cheetah C model), as well as new electronics and weaponry. The Mirage III dates from approximately the same time period as the F-106, and is broadly comparable in performance, so such a project should be (theoretically) feasible.
Calling our new aircraft the F-106M, we can start by looking at what we don't need. The fairly extensive electronics fit allowing the F-106A to interface with the SemiAutomatic Ground Environment (SAGE) is redundant, so it can go. That should save us a couple hundred kilos, and free up some space. Equipment needed for the carriage of nuclear weapons (such as the AIR-2) can also get removed. In its place an autocannon such as the M61 can be permanently fitted.
Though the F-106 was originally designed as an interceptor, it actually has decent turning ability, at least at high speeds. However, at low speeds, the aircraft tends to lose energy. This tends to be an issue inherent with dynamically stable pure deltas, such as the F-106. One option to improve lift at low speeds and high angles of attack would be to fit canards, such as on the AJ37. This would require extensive modification to the forward fuselage and air intakes of the aircraft. Another option would be to fit leading edge extensions to the wings, as are found on the F-18. These leading edge extensions generate vortices, which increase lift at high angles of attack. Additionally, they would shift the center of lift forward, reducing the static margin of the aircraft and improving performance. (Here's a brief explanation of why instability is good in an aircraft.) Another benefit would be reduction of takeoff distance, i
The second major change is in the powerplant. The J75 is not a bad engine by any means, but by 1980 it's getting quite long in the tooth. If possible, we should re-engine the F-106M with a newer powerplant. One of the best candidates is the Pratt & Whitney F100. Though the F100 is about a meter longer than the J75, it is only 9 cm larger in diameter. Given that the structure of our improved F-106M will be undergoing a substantial refurbishment, increasing the diameter of the engine bay and lengthening the fuselage slightly should not be an insurmountable obstacle. In fact, the largest challenge would probably be redesigning the intakes to accommodate the F100. Obviously, some sort of variable geometry intake should be retained, to take advantage of the F-106's exceptional speed (variable geometry intakes are virtually essential for speeds about Mach 2).
In exchange for all this trouble, the F100 gives us significantly improved fuel consumption compared to the J75. Additionally, the F100 has a thrust to weight ratio about double that of the J75, so it ends up weighing about half as much. With the weight of the F-106M reduced by up to 1,000 kilograms compared to the base model, range will be improved, as will the maneuverability of the aircraft (thanks to reduced wing loading).
Most of the other changes are internal. An improved radar would be essential, as the F-106s aging 1950s era fire control systems were designed to target large, slow targets at extreme range in conjunction with ground control, rather than air superiority operations. One candidate would be the AN/APG-63, which was fitted to early model F-15s. Whether this or another radar is used, it is likely that a redesign of the nose section would be required (as was planned for the F-106C, which would have been fitted with the radar from the aborted XF-108 program). Avionics for ground attack would also be essential, in order to give the F-106M true multirole capability. These could be fitted in place of the deleted SAGE equipment found on the F-106A. Not only would this include fitting a modern bomb sight, but compatibility with guided munitions such as the GBU-12. In order to allow the F-106M to utilize laser guided munitions, it could be possible to give the aircraft a built-in laser designator. However, a more likely option would be the fitting of a targeting pod to one of the underwing hardpoints on appropriate missions.
Additionally, compatibility with modern weapons, such as all aspect variants of the AIM-9 and AIM-7. A helmet mounted sight (as developed by the South Africans in the 1970s), when coupled with an all-aspect IR missile would result in a massive increase in dog fighting capability. This would keep the F-106M viable in a close in fight, despite its inferiority in this arena against designs such as the MiG-29 or F-16.
Numerous other, smaller changes could be made, such as replacing the old ejection seats with an improved model, and fitting a new RWR. While completely rebuilding an F-106 into a 4th generation fighter was never likely to happen, it's interesting to look at whether such an undertaking might have been possible at all.
Suppose that, at sometime around 1980 a country using the F-106 wanted to modify them such that they could be used in the air superiority role for at least another decade. How would they go about doing this?
Those of you who are more reasonable might ask why the country in question doesn't just buy a bunch of upgraded F-4s or MiG-23s (or even some F-15s or 16s) and use them instead. Well, they could, but that would be a quite boring end to this post.
I'm going to use the development of the Atlas Cheetah as a model for our F-106 improvement program. The Cheetah was developed by apartheid-era South Africa from their existing Mirage III airframes, and involved a quite extensive rework of the aircraft, including a complete rebuild of the airframe, fitting of an upgraded engine (in the Cheetah C model), as well as new electronics and weaponry. The Mirage III dates from approximately the same time period as the F-106, and is broadly comparable in performance, so such a project should be (theoretically) feasible.
Calling our new aircraft the F-106M, we can start by looking at what we don't need. The fairly extensive electronics fit allowing the F-106A to interface with the SemiAutomatic Ground Environment (SAGE) is redundant, so it can go. That should save us a couple hundred kilos, and free up some space. Equipment needed for the carriage of nuclear weapons (such as the AIR-2) can also get removed. In its place an autocannon such as the M61 can be permanently fitted.
Though the F-106 was originally designed as an interceptor, it actually has decent turning ability, at least at high speeds. However, at low speeds, the aircraft tends to lose energy. This tends to be an issue inherent with dynamically stable pure deltas, such as the F-106. One option to improve lift at low speeds and high angles of attack would be to fit canards, such as on the AJ37. This would require extensive modification to the forward fuselage and air intakes of the aircraft. Another option would be to fit leading edge extensions to the wings, as are found on the F-18. These leading edge extensions generate vortices, which increase lift at high angles of attack. Additionally, they would shift the center of lift forward, reducing the static margin of the aircraft and improving performance. (Here's a brief explanation of why instability is good in an aircraft.) Another benefit would be reduction of takeoff distance, i
The second major change is in the powerplant. The J75 is not a bad engine by any means, but by 1980 it's getting quite long in the tooth. If possible, we should re-engine the F-106M with a newer powerplant. One of the best candidates is the Pratt & Whitney F100. Though the F100 is about a meter longer than the J75, it is only 9 cm larger in diameter. Given that the structure of our improved F-106M will be undergoing a substantial refurbishment, increasing the diameter of the engine bay and lengthening the fuselage slightly should not be an insurmountable obstacle. In fact, the largest challenge would probably be redesigning the intakes to accommodate the F100. Obviously, some sort of variable geometry intake should be retained, to take advantage of the F-106's exceptional speed (variable geometry intakes are virtually essential for speeds about Mach 2).
In exchange for all this trouble, the F100 gives us significantly improved fuel consumption compared to the J75. Additionally, the F100 has a thrust to weight ratio about double that of the J75, so it ends up weighing about half as much. With the weight of the F-106M reduced by up to 1,000 kilograms compared to the base model, range will be improved, as will the maneuverability of the aircraft (thanks to reduced wing loading).
Most of the other changes are internal. An improved radar would be essential, as the F-106s aging 1950s era fire control systems were designed to target large, slow targets at extreme range in conjunction with ground control, rather than air superiority operations. One candidate would be the AN/APG-63, which was fitted to early model F-15s. Whether this or another radar is used, it is likely that a redesign of the nose section would be required (as was planned for the F-106C, which would have been fitted with the radar from the aborted XF-108 program). Avionics for ground attack would also be essential, in order to give the F-106M true multirole capability. These could be fitted in place of the deleted SAGE equipment found on the F-106A. Not only would this include fitting a modern bomb sight, but compatibility with guided munitions such as the GBU-12. In order to allow the F-106M to utilize laser guided munitions, it could be possible to give the aircraft a built-in laser designator. However, a more likely option would be the fitting of a targeting pod to one of the underwing hardpoints on appropriate missions.
Additionally, compatibility with modern weapons, such as all aspect variants of the AIM-9 and AIM-7. A helmet mounted sight (as developed by the South Africans in the 1970s), when coupled with an all-aspect IR missile would result in a massive increase in dog fighting capability. This would keep the F-106M viable in a close in fight, despite its inferiority in this arena against designs such as the MiG-29 or F-16.
Numerous other, smaller changes could be made, such as replacing the old ejection seats with an improved model, and fitting a new RWR. While completely rebuilding an F-106 into a 4th generation fighter was never likely to happen, it's interesting to look at whether such an undertaking might have been possible at all.
Tuesday, September 8, 2015
This Blog Isn't Dead
After a long hiatus, I've decided to get back into this. Hopefully I'll stick with it.
In the meantime, I've rearranged some of the sidebars a bit. Go ahead and check out some of the links I've added.
In the meantime, I've rearranged some of the sidebars a bit. Go ahead and check out some of the links I've added.
Subscribe to:
Posts (Atom)